Teorema d'isomorfisme

En matemàtiques, i més específicament en l'àmbit de l'àlgebra abstracta, els teoremes d'isomorfisme són tres teoremes que descriuen la relació entre quocients, homomorfismes i subobjectes. Existeixen diferents versions dels teoremes per a grups, anells, espais vectorials, mòduls, àlgebres de Lie i altres estructures algebraiques. En àlgebra universal, els teoremes d'isomorfisme es poden generalitzar a l'àmbit d'àlgebres i congruències.

Història

Els teoremes d'isomorfisme foren enunciats per primer cop per al cas de morfismes de mòduls per la matemàtica Emmy Noether en la seva publicació Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern del 1927 als Mathematische Annalen. Es poden trobar altres resultats menys generals d'aquests teoremes a l'obra de Richard Dedekind i a publicacions anteriors de Noether.

Tres anys més tard, Bartel van der Waerden publicà la seva obra Algebra, el primer tractat d'àlgebra abstracta que introduí l'aproximació grups-anells-cossos. Van der Waerden basà part de la seva obra en exposicions de Noether sobre teoria de grups i d'Emil Artin sobre àlgebra, així com en un seminari conduït per Artin, Wilhelm Blaschke, Otto Schreier, i el propi van der Waerden sobre ideals. Els tres teoremes d'isomorfisme, anomenats teorema d'homomorfisme, i les dues lleis d'isomorfisme quan s'apliquen a grups, apareixen explícitament a l'obra de van der Waerden.

Grups

Enunciem primer els tres teoremes per al cas de grups. Notem que algunes fonts intercanvien l'ordre dels teoremes segon i tercer.^[1] Una altra variant que es pot trobar a la bibliografia, particularment a l'Algebra de van der Waerden, és anomenar Teorema Fonamental d'Homomorfisme al primer teorema d'isomorfisme, i llavors reduir a dos el nombre de teoremes d'isomorfisme restants.^[2] D'altra banda, alguns autors consideren que el teorema del reticle (també conegut com el teorema de correspondència) és el quart teorema d'isomorfisme.

Primer teorema d'isomorfisme

Siguin G i G' dos grups, i sigui f: G → G' un homomorfisme. Aleshores:

1. El nucli de f és un subgrup normal de G,
2. La imatge de f és un subgrup de G', i
3. La imatge de f és isomorfa al grup quocient G / Ker(f).

En particular, si f és exhaustiva, llavors G' és isomorf a G / Ker(f).^[3]

Segon teorema d'isomorfisme

Sigui G un grup. Sigui H un subgrup de G, i sigui N un subgrup normal de G. Aleshores:

1. El conjunt producte HN és un subgrup de G,
2. La intersecció H ∩ N és un subgrup normal de H, i
3. Els grups quocient (HN) / N i H / (H ∩ N) són isomorfs.

Aquest segon teorema d'isomorfisme es dedueix del primer, ja que ai ${\displaystyle N}$ és normal a G, llavors també ${\displaystyle H\cap N}$ és normal a ${\displaystyle H}$, i es pot demostrar que l'epimorfisme

${\displaystyle {\begin{array}{cccc}\varphi :&H&\longrightarrow &(HN)/N\\&h&\longmapsto &HN\end{array}}}$

verifica ${\displaystyle \ker \varphi =H\cap N}$. Si ${\displaystyle \pi :HN\longrightarrow HN/N}$ i ${\displaystyle \rho :H\longrightarrow H/(H\cap N)}$ són projeccions canòniques, llavors la construcció de l'isomorfisme ${\displaystyle \psi :H/(H\cap N)\longrightarrow NH/N}$ es descriu pel diagrama commutatiu de la figura.

Alguns autors anomenen aquest teorema d'isomorfisme el "teorema diamant", a causa de la forma del reticle de subgrups resultant, amb HN al capdamunt, H ∩ N a la part inferior, i amb N i H als costats.^[4] Altres autors també l'anomenen "llei del paral·lelogram" (per analogia amb la llei del paral·lelogram per a vectors) perquè, en el reticle de subgrups, els dos costats que representen els grups quocients (SN) / N i S / (S ∩ N) són "iguals", en el sentit que són isomorfs.^[5]

Tercer teorema d'isomorfisme

Sigui G un grup, i sigui N un subgrup normal de G. Aleshores

1. Si ${\displaystyle H}$ és un subgrup de ${\displaystyle G}$ tal que ${\displaystyle N\subseteq H\subseteq G}$, llavors ${\displaystyle H/N}$ és un subgrup de ${\displaystyle G/N}$.
2. Tot subgrup de ${\displaystyle G/N}$ és de la forma ${\displaystyle H/N}$, per a algun subgrup ${\displaystyle H}$ de ${\displaystyle G}$ tal que ${\displaystyle N\subseteq H\subseteq G}$.
3. Si ${\displaystyle H}$ és un subgrup normal de ${\displaystyle G}$ tal que ${\displaystyle N\subseteq H\subseteq G}$, llavors ${\displaystyle H/N}$ és un subgrup normal de ${\displaystyle G/N}$.
4. Tot subgrup normal de ${\displaystyle G/N}$ és de la forma ${\displaystyle H/N}$, per a algun subgrup normal ${\displaystyle H}$ de ${\displaystyle G}$ tal que ${\displaystyle N\subseteq H\subseteq G}$.
5. Si ${\displaystyle H}$ és un subgrup normal de ${\displaystyle G}$ tal que ${\displaystyle N\subseteq H\subseteq G}$, llavors el grup quocient ${\displaystyle (G/N)/(H/N)}$ és isomorf a ${\displaystyle G/H}$.

Això dona lloc al següent diagrama commutatiu:

on ${\displaystyle \varphi _{1},\varphi _{2}}$ són projeccions canòniques, ${\displaystyle {\mbox{id}}\,\!}$ és l'aplicació identitat, i les fletxes horitzontals formen una successió d'homomorfismes exacta.

Hom pot visualitzar l'enunciat d'aquest teorema com que es pot "cancel·lar el denominador N", encara que això no és formalment correcte.

Discussió

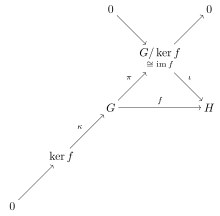
El primer teorema d'isomorfisme és una conseqüència del resultat de la teoria de categories de què la categoria de grups és (normal epi, mono)-factoritzable; en altres paraules, els epimorfismes normals i els monomorfismes formen un sistema de factorització per a la categoria. El diagrama commutatiu de la figura il·lustra aquest fet, que mostra els objectes i morfismes que es poden deduir a partir del morfisme f: G→H. Aquest diagrama mostra que tot morfisme de la categoria de grups té un nucli en el sentit de la teoria de categories; un morfisme qualsevol f factoritza en ${\displaystyle \iota \circ \pi }$, on ι és un monomorfisme i π és un epimorfisme (en una categoria conormal, tot epimorfisme és normal). Això es representa en el diagrama mitjançant un objecte ${\displaystyle \ker f}$ i un monomorfisme ${\displaystyle \kappa :\ker f\rightarrow G}$ (els nuclis són sempre monomorfismes), que completen la successió exacta curta que va des de la part inferior esquerra a la part superior dreta del diagrama. L'ús de la convenció de les seqüències exactes ens estalvia haver de representar els morfismes zero de ${\displaystyle \ker f}$ a H i ${\displaystyle G/\ker f}$.

Si la successió és separable per la dreta (és a dir, si hi ha un morfisme σ que envia ${\displaystyle G/\ker f}$ a una π-preimatge de si mateix), llavors G és el producte semidirecte del subgrup normal ${\displaystyle \operatorname {im} \kappa }$ i el subgrup ${\displaystyle \operatorname {im} \sigma }$. Si és separable per l'esquerra (és a dir, si existeix algun ${\displaystyle \rho :G\rightarrow \ker f}$ tal que ${\displaystyle \rho \circ \kappa =\operatorname {id} _{\ker f}}$), llavors també ha de ser separable per la dreta, i ${\displaystyle \operatorname {im} \kappa \times \operatorname {im} \sigma }$ és una descomposició en producte directe de G. En general, l'existència d'una separació per la dreta no implica l'existència d'una separació per l'esquerra; però en una categoria abeliana (com la dels grups abelians), les separacions per l'esquerra i per la dreta són equivalents pel lema de separació, i és suficient tenir una separació per la dreta per tenir una descomposició en suma directa ${\displaystyle \operatorname {im} \kappa \oplus \operatorname {im} \sigma }$. En una categoria abeliana, tot monomorfisme és normal, i es pot estendre el diagrama amb una segona successió exacta curta ${\displaystyle 0\rightarrow G/\ker f\rightarrow H\rightarrow \operatorname {coker} f\rightarrow 0}$.

Pel que fa al segon teorema d'isomorfisme, el producte SN és el suprem de S i N en el reticle de subgrups de G, mentre que la intersecció S ∩ N n'és l'ínfim.

Es pot generalitzar el tercer teorema d'isomorfisme mitjançant el lema dels nou en categories abelianes.

Anells

Els enunciats dels teoremes per a anells són similars, amb el concepte de subgrup normal reemplaçat pel d'ideal.

Primer teorema d'isomorfisme

Siguin R i S dos anells, i sigui φ: R → S un homomorfisme d'anells. Aleshores:

1. El nucli de φ és un ideal de R,
2. La imatge de φ és un subanell de S, i
3. La imatge de φ és isomorfa a l'anell quocient R / ker(φ).

En particular, si φ és exhaustiva, llavors S és isomorf a R / ker(φ).

Segon teorema d'isomorfisme

Sigui R un anell. Siguin S un subanell de R i I un ideal de R. Aleshores:

1. La suma S + I = {s + i | s ∈ S, i ∈ I} és un subanell de R,
2. La intersecció S ∩ I és un ideal de S, i
3. Els anells quocient (S + I) / I i S / (S ∩ I) són isomorfs.

Tercer teorema d'isomorfisme

Siguin R un anell, i B un ideal de R. Aleshores

1. Si ${\displaystyle A}$ és un subanell de ${\displaystyle R}$ tal que ${\displaystyle B\subseteq A\subseteq R}$, llavors ${\displaystyle A/B}$ és un subanell de ${\displaystyle R/B}$.
2. Tot subanell de ${\displaystyle R/B}$ és de la forma ${\displaystyle A/B}$, per a algun subanell ${\displaystyle A}$ de ${\displaystyle R}$ tal que ${\displaystyle B\subseteq A\subseteq R}$.
3. Si ${\displaystyle A}$ és un ideal de ${\displaystyle R}$ tal que ${\displaystyle B\subseteq A\subseteq R}$, llavors ${\displaystyle A/B}$ és un ideal de ${\displaystyle R/B}$.
4. Tot ideal de ${\displaystyle R/B}$ és de la forma ${\displaystyle A/B}$, per a algun ideal ${\displaystyle A}$ de ${\displaystyle R}$ tal que ${\displaystyle B\subseteq A\subseteq R}$.
5. Si ${\displaystyle A}$ és un ideal de ${\displaystyle R}$ tal que ${\displaystyle B\subseteq A\subseteq R}$, llavors l'anell quocient ${\displaystyle (R/B)/(A/B)}$ és isomorf a ${\displaystyle R/A}$.

Mòduls

Els enunciats dels teoremes d'isomorfisme per a mòduls són particularment senzills, ja que és possible formar un mòdul quocient a partir d'un submòdul qualsevol. Els teoremes d'isomorfisme per a espais vectorials i per a grups abelians són casos particulars dels resultats per a mòduls. Per a espais vectorials de dimensió finita, aquests teoremes són una conseqüència del teorema del rang.

En els teoremes següents, el terme “mòdul” vol dir “R-mòdul”, on R és un anell fixat.

Primer teorema d'isomorfisme

Siguin M i N dos mòduls, i sigui φ: M → N un homomorfisme de mòduls. Aleshores:

1. El mòdul de φ és un submòdul de M,
2. La imatge de φ és un submòdul de N, i
3. La imatge de φ és isomorfa al mòdul quocient M / ker(φ).

En particular, si φ és exhaustiva, llavors N és isomorf a M / ker(φ).

Segon teorema d'isomorfisme

Sigui M un mòdul, i siguin S i T dos submòduls de M. Aleshores:

1. La suma S + T = {s + t | s ∈ S, t ∈ T} és un submòdul de M,
2. La intersecció S ∩ T és un submòdul de M, i
3. Els mòduls quocient (S + T) / T i S / (S ∩ T) són isomorfs.

Tercer teorema d'isomorfisme

Sigui M un mòdul, i sigui T un submòdul de M.

1. Si ${\displaystyle S}$ és un submòdul de ${\displaystyle M}$ tal que ${\displaystyle T\subseteq S\subseteq M}$, llavors ${\displaystyle S/T}$ és un submòdul de ${\displaystyle M/T}$.
2. Tot submòdul de ${\displaystyle M/T}$ és de la forma ${\displaystyle S/T}$, per a algun submòdul ${\displaystyle S}$ de ${\displaystyle M}$ tal que ${\displaystyle T\subseteq S\subseteq M}$.
3. Si ${\displaystyle S}$ és un submòdul de ${\displaystyle M}$ tal que ${\displaystyle T\subseteq S\subseteq M}$, llavors el mòdul quocient ${\displaystyle (M/T)/(S/T)}$ és isomorf a ${\displaystyle M/S}$.

General

Per tal de generalitzar aquests resultats a una àlgebra universal, cal substituir els subgrups normals per congruències.

Una congruència sobre una àlgebra ${\displaystyle A}$ és una relació d'equivalència ${\displaystyle \Phi }$ que és una subàlgebra de ${\displaystyle A\times A}$ dotada amb l'estructura d'operació component a component. Hom pot definir el conjunt de classes d'equivalència ${\displaystyle A/\Phi }$ sobre una àlgebra del mateix tipus, si es defineixen les operacions mitjançant elements representatius; això està ben definit perquè ${\displaystyle \Phi }$ és una subàlgebra de ${\displaystyle A\times A}$. L'estructura resultant és l'àlgebra quocient.

Primer teorema d'isomorfisme

Sigui ${\displaystyle f:A\rightarrow B}$ un homomorfisme d'àlgebres. Llavors la imatge de ${\displaystyle f}$ és una subàlgebra de ${\displaystyle B}$, la relació donada per ${\displaystyle \Phi :f(x)=f(y)}$ (és a dir, el nucli de f) és una congruència sobre ${\displaystyle A}$, i les àlgebres ${\displaystyle \ A/\Phi \ }$ i ${\displaystyle {\text{im}}\ f}$ són isomorfes. (Notem que, en el cas d'un grup, f(x)=f(y) si i només si f(xy^-1) = 1, amb la qual cosa hom recupera la noció de nucli emprada en teoria de grups.)

Segon teorema d'isomorfisme

Donades una àlgebra ${\displaystyle A}$, una subàlgebra ${\displaystyle B}$ De ${\displaystyle A}$, i una congruència ${\displaystyle \Phi }$ sobre ${\displaystyle A}$, sigui ${\displaystyle \Phi _{B}=\Phi \cap (B\times B)}$ la traça de ${\displaystyle \Phi }$ dins ${\displaystyle B}$ i ${\displaystyle [B]^{\Phi }=\{K\in A/\Phi :K\cap B\neq \emptyset \}}$ la col·lecció de classes d'equivalència que intersecten amb ${\displaystyle B}$. Aleshores:

1. ${\displaystyle \Phi _{B}}$ és una congruència sobre ${\displaystyle B}$,
2. ${\displaystyle \ [B]^{\Phi }}$ és una subàlgebra de ${\displaystyle A/\Phi }$, i
3. L'àlgebra ${\displaystyle [B]^{\Phi }}$ és isomorfa a l'àlgebra ${\displaystyle B/\Phi _{B}}$.

Tercer teorema d'isomorfisme

Sigui ${\displaystyle A}$ una àlgebra i siguin ${\displaystyle \Phi ,\Psi }$ dues relacions de congruència sobre ${\displaystyle A}$ tals que ${\displaystyle \Psi \subseteq \Phi }$. Aleshores ${\displaystyle \Phi /\Psi =\{([a']_{\Psi },[a'']_{\Psi }):(a',a'')\in \Phi \}=[\ ]_{\Psi }\circ \Phi \circ [\ ]_{\Psi }^{-1}}$ és una congruència sobre ${\displaystyle A/\Psi }$, i ${\displaystyle A/\Phi }$ és isomorf a ${\displaystyle (A/\Psi )/(\Phi /\Psi )}$.

Referències

Bibliografia

• Noether, Emmy «Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern». Mathematische Annalen. Springer-Verlag, 96, 1927, pàg. 26-6. DOI: 10.1007/BF01209152. ISSN: 0025-5831.
• McLarty, Colin. «Emmy Noether’s ‘Set Theoretic’ Topology: From Dedekind to the rise of functors». The Architecture of Modern Mathematics: Essays in history and philosophy (edited by Jeremy Gray and José Ferreirós), Oxford University Press (2006) p. 211–35.
• Jacobson, Nathan. Basic algebra. 2. 2a edició. Dover, 2009. ISBN 978-0-486-47187-7. 
• Cohn, Paul M. «Chapter II.3». A: Universal algebra. Springer, 1981, p. 57. ISBN 9027712549. 

Enllaços externs

• Primer teorema d'isomorfisme a PlanetMath. Demostració a PlanetMath
• Segon teorema d'isomorfisme a PlanetMath. Demostració a PlanetMath
• Tercer teorema d'isomorfisme a PlanetMath. Demostració a PlanetMath