Relleno con círculos de un triángulo equilátero

El relleno con círculos de un triángulo equilátero es un problema de empaquetado estudiado en matemáticas discretas. Consiste en acomodar n círculos de radio unidad en el triángulo equilátero más pequeño posible.

Soluciones

Se conocen las soluciones óptimas para n < 13 y para cualquier número triangular de círculos, y en los años 1990 se formularon conjeturas para n < 28.[1]​[2]​[3]​

Una conjetura de Paul Erdős y Norman Oler indica que, si n es un número triangular, entonces los empaquetamientos óptimos de los n−1 y de los n círculos tienen la misma longitud lateral: es decir, según la conjetura, se puede encontrar un empaquetamiento óptimo para n−1 círculos eliminando cualquier círculo individual del empaquetamiento hexagonal óptimo para n círculos.[4]​ Esta conjetura ahora se sabe que es verdadera para n ≤ 15.[5]​

Soluciones mínimas y su longitud del lado del triángulo asociado para círculos de radio uno:[1]​

Número de
círculos 		Número
triangular 		Longitud Área
1 Sí 2 3 {\displaystyle 2{\sqrt {3}}} = 3.464... 5.196...
2 No 2 + 2 3 {\displaystyle 2+2{\sqrt {3}}} = 5.464... 12.928...
3 Sí 2 + 2 3 {\displaystyle 2+2{\sqrt {3}}} = 5.464... 12.928...
4 No 4 3 {\displaystyle 4{\sqrt {3}}} = 6.928... 20.784...
5 No 4 + 2 3 {\d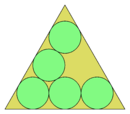isplaystyle 4+2{\sqrt {3}}} = 7.464... 24.124...
6 Sí 4 + 2 3 {\displaystyle 4+2{\sqrt {3}}} = 7.464... 24.124...
7 No 2 + 4 3 {\displaystyle 2+4{\sqrt {3}}} = 8.928... 34.516...
8 No 2 + 2 3 + 2 3 33 {\displaystyle 2+2{\sqrt {3}}+{\dfrac {2}{3}}{\sqrt {33}}} = 9.293... 37.401...
9 No 6 + 2 3 {\displaystyle 6+2{\sqrt {3}}} = 9.464... 38.784...
10 Sí 6 + 2 3 {\displaystyle 6+2{\sqrt {3}}} = 9.464... 38.784...
11 No 4 + 2 3 + 4 3 6 {\displaystyle 4+2{\sqrt {3}}+{\dfrac {4}{3}}{\sqrt {6}}} = 10.730... 49.854...
12 No 4 + 4 3 {\displaystyle 4+4{\sqrt {3}}} = 10.928... 51.712...
13 No 4 + 10 3 3 + 2 3 6 {\displaystyle 4+{\dfrac {10}{3}}{\sqrt {3}}+{\dfrac {2}{3}}{\sqrt {6}}} = 11.406... 56.338...
14 No 8 + 2 3 {\displaystyle 8+2{\sqrt {3}}} = 11.464... 56.908...
15 Sí 8 + 2 3 {\displaystyle 8+2{\sqrt {3}}} = 11.464... 56.908...

Un problema estrechamente relacionado es cubrir el triángulo equilátero con un número fijo de círculos iguales, teniendo un radio tan pequeño como sea posible.[6]​

Véase también

Referencias

  1. ↑ a b Melissen, Hans (1993), «Densest packings of congruent circles in an equilateral triangle», American Mathematical Monthly 100 (10): 916-925, MR 1252928, doi:10.2307/2324212 ..
  2. ↑ Melissen, J. B. M.; Schuur, P. C. (1995), «Packing 16, 17 or 18 circles in an equilateral triangle», Discrete Mathematics 145 (1-3): 333-342, MR 1356610, doi:10.1016/0012-365X(95)90139-C ..
  3. ↑ Graham, R. L.; Lubachevsky, B. D. (1995), «Dense packings of equal disks in an equilateral triangle: from 22 to 34 and beyond», Electronic Journal of Combinatorics 2: Article 1, approx. 39 pp. (electronic), MR 1309122 ..
  4. ↑ Oler, Norman (1961), «A finite packing problem», Canadian Mathematical Bulletin 4: 153-155, MR 0133065, doi:10.4153/CMB-1961-018-7 ..
  5. ↑ Payan, Charles (1997), «Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler», Discrete Mathematics (en francés), 165/166: 555-565, MR 1439300, doi:10.1016/S0012-365X(96)00201-4 ..
  6. ↑ Nurmela, Kari J. (2000), «Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles», Experimental Mathematics 9 (2): 241-250, MR 1780209, doi:10.1080/10586458.2000.10504649 ..
Control de autoridades
  • Proyectos Wikimedia
  • Wd Datos: Q5121502
  • Wd Datos: Q5121502