Thaleen lause

Thaleen lause on geometrian lause, jonka mukaan puoliympyrän sisältämä kehäkulma on suora. Sama voidaan sanoa toisinkin. Jos kolmion yksi sivu on ympyrän halkaisijalla ja yksi kärjistä ympyrän kehällä, on tämä kulma aina suora. Thaleen lause on kehäkulmalauseen erikoistapaus, kun keskuskulmaksi valitaan oikokulma eli 180°, jolloin kehäkulmaksi tulee 90°.^[1][2]

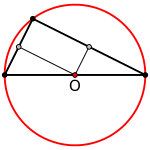
Käyttämällä kolmion sivuja suuntana, voidaan kolmio jakaa janoilla osiin (kuva vasemmalla). Koska kehäpisteessä kulma on suora, syntyy erikoinen tilanne. Halkaisijan keskipisteestä, joka on samalla ympyrän keskipiste, vedetään sivuja vasten normaalit, jotka osuvat sivujen keskipisteisiin. Tämä vastaa tilannetta, jossa pedaalipistettä O vastaavat kolmion sivujen kantapisteet ovat kolmion keskinormaaleina. Kuviosta erottuu suorakulmio ja kaksi kolmiota. Kolmiot ovat referenssikolmion kanssa yhdenmuotoiset, mutta kooltaan puolet pienempiä.

Kolmio ${\displaystyle \triangle OAB}$ on tasakylkinen kolmio, sillä sivut OA ja OB ovat ympyrän säteitä ja siksi yhtäpitkät (kuva oikealla). Silloin kantakulmat ${\displaystyle \measuredangle OAB}$ ja ${\displaystyle \measuredangle ABO}$ ovat yhtäsuuret. Merkitään ne α. Samasta syystä kolmio ${\displaystyle \triangle OBC}$ on tasakylkinen, joten merkitään samansuuruiset kulmat ${\displaystyle \measuredangle BCO}$ ja ${\displaystyle \measuredangle OBC}$ luvulla β. Kulma ${\displaystyle \measuredangle ABC}$ tiedetään suoraksi kulmaksi, joten sen jakavat kulmat ovat komplementtikulmia eli α + β = 90°. Vaikuttaa siltä, että kehäpisteen eri asemat ympyrän kehällä, antavat kaikki molemmille kulmille kaikki kulmamitat 0°−90°.

Ympyrän ulkopuolisesta pisteestä P vedetään ympyrälle kaksi tangenttia, jotka sivuavat sitä pisteissä T ja T'. Thaleen lauseella voidaan löytää sivuamispisteet, kun tiedetään kulmien ${\displaystyle \measuredangle PT'O}$ ja ${\displaystyle \measuredangle OTP}$ olevan suoria. Etsitään (harpilla ja viivaimella) janan OP keskipiste H, josta mitataan ympyrän säteeksi HP tai HO. Piirretään ympyrä, joka leikkaa alkuperäistä ympyrää kahdessa pisteessä T ja T'. Näissä pisteissä kulmat ovat suoria, koska ne ovat ympyrän kehällä (Thaleen lause), joten näissä pisteissä sivuavat myös tangentit. Tangentithan ovat kohtisuorassa säteitä vastaan.

Seuraavassa todistetaan sekä Thaleen lause että käänteisen Thaleen lauseen tulos.

Thaleen lause: Jos kolmion kaksi kärkeä ovat ympyrän halkaisijan päätepisteet ja kolmas kärki on ympyrän kehällä, on viimeinen kulma suorakulma.

Olkoon ${\displaystyle \triangle ABC}$ ympyrän sisään piirretty kolmio, missä AC on ympyrän halkaisija. Olkoon O tämän ympyrän keskipiste. Piirretään ympyrän säde OB. Nyt kolmiot ${\displaystyle \triangle AOB}$ ja ${\displaystyle \triangle BOC}$ ovat tasakylkisiä, sillä kummassakin kolmiossa on sivuinaan kaksi ympyrän sädettä. Siten pätee ${\displaystyle \measuredangle CAB=\measuredangle ABO}$, ${\displaystyle \measuredangle BCA=\measuredangle OBC}$ ja ${\displaystyle \measuredangle ABC=\measuredangle CAB+\measuredangle BCA}$. Toisaalta ${\displaystyle \measuredangle ABC+\measuredangle CAB+\measuredangle BCA=180^{\circ }}$, joten ${\displaystyle \measuredangle ABC=90^{\circ }}$.

Käänteinen Thaleen lause: Suorakulmaisen kolmion hypotenuusa on kolmion ympäri piirretyn ympyrän halkaisijalla.

Piirretään suorakulmaisen kolmion ${\displaystyle \triangle ABC}$ viereen sen kanssa yhtenevä kolmio ${\displaystyle \triangle CAD}$ siten, että hypotenuusat AC sivuavat toisensa ja että vastinsivut (AB ja CD sekä BC ja AD) tulevat toistensa vastakkaisille sivuille. Koska vastinsivut ovat nelikulmiossa toisiaan vastapäätä, on muodostunut nelikulmio suunnikas.

Suunnikkaassa vastakkaiset kulmat ovat yhtäsuuret ja viereiset kulmat toistensa komplementtikulmat. Suunnikas muodostettiin suorakulmaisista kolmioista, joten yhdet kulmat (${\displaystyle \measuredangle CBA}$ ja ${\displaystyle \measuredangle ADC}$) ovat suoria kulmia. Koska suoran kulman supplementtikulma on myös suora kulma, on suunnikas lisäksi suorakulmio.

Suunnikkaassa lävistäjät AC ja BD puolittavat toisensa ja suorakulmiossa lävistäjät ovat yhtä pitkät. Silloin lävistäjien puolikkaat ovat kaikki yhtäpitkät. Jos nimitetään lävistäjien leikkauspisteeksi O ja kaikki neljä lävistäjän puolikasta (OA, OB, OC ja OD) säteiksi, voidaan piirtää ympyrä, joka ympäröi nelikulmion.

Tämän nelikulmion lävistäjä AC on myös kolmion hypotenuusa, jolla sijaitsee kaksi kehäpistettä A ja C ja ympyrän keskipiste O. Koska hypotenuusa AOC on suora jana, on se samalla ympyrän halkaisija.

Edelliset kaksi todistusta riittävät perusteluiksi seuraavaan Thaleen ja sen käänteiseen lauseeseen: Kolmion ympäri piirretyn ympyrän halkaisija on yksi kolmion sivuista jos ja vain jos kolmio on suorakulmainen kolmio.

Thaleen lause liitetään antiikin kreikkalaisen mytologian mukaan Thaleen (noin 625 − noin 547 eaa.), joka eli Miletoksessa kauppiaana. Hän on ilmeisesti matkustanut Kaksoisvirran maassa kaldealaisen hallitsijan Nebukadnessarin aikana ja on tutustunut sikäläiseen tähtitieteen taulukoihin ja instrumentteihin. Hän on hämmästyttänyt maanmiehiään esittämällä erilaisia teoreemoja, jotka hän on perustellut pätevästi. Teoreemojen joukossa on perimätiedon mukaan ollut myös puoliympyrän sisään muodostuva suora kulma.^[3][4]

Tämä tieto ei kuitenkaan keksitty esihelleenisessä Kreikassa, vaan se tunnettiin yli 1 000 vuotta aikaisemmin babylonialaisessa matematiikassa. Heidän savitauluistaan, joita kirjoitettiin nuolenpäämerkeillä, on löydetty tästä aiheesta laskutehtäviä. Intialaiset omaksuivat Thaleen lauseen heiltä.^[5] Egyptiläisten jäljelle jääneistä papyruksista tätä ongelmaa ei ole löydetty.^[6] Eukleides käsitteli lausetta kirjassaan Alkeet (III kirja, 31. väite).^[7]

• Nimekästä geometriaa (Arkistoitu – Internet Archive), lause todistuksineen suomeksi

• Kuvia tai muita tiedostoja aiheesta Thaleen lause Wikimedia Commonsissa