Egységtávolsággráf

A matematika, azon belül a geometriai gráfelmélet területén az egységtávolsággráf vagy egység távolságú gráf (unit distance graph) olyan gráf, ami az euklideszi síkon lévő pontokon felrajzolható oly módon, hogy két csúcspont akkor van éllel összekötve, ha a közöttük lévő távolság éppen 1. Az egységtávolsággráfok élei metszhetik egymást, tehát nem feltétlenül síkba rajzolható gráfok; a metszések nélkül azonos élhosszal síkba rajzolható gráf neve gyufagráf.

A Hadwiger–Nelson-probléma felveti az egység távolságú gráfok kromatikus számának kérdését. Ismertek négy színnel színezhető egységtávolsággráfok, és azt is tudjuk, hogy minden ilyen gráf legfeljebb hét színnel színezhető.

Egy másik fontos nyitott kérdés, hogy az egység távolságú gráfoknak hány élük lehet csúcspontjaik számának arányában.

A következő gráfok egységtávolsággráfok:

• Bármely körgráf
• Bármely rácsgráf (csempézési gráf)
• Bármely hiperkockagráf
• Bármely csillaggráf
• A Petersen-gráf
• A Heawood-gráf (Gerbracht 2009)
• A W₇ kerékgráf
• a Moser-rokka, a legkisebb 4 színnel színezhető egységtávolsággráf

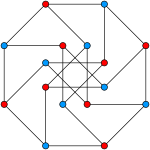
Egyes szerzők egységtávolsággráfnak tekintenek minden gráfot, ha csúcsai elhelyezhetők egy síkban oly módon, hogy a szomszédos csúcspárok egységnyi távolságra legyenek, nem foglalkozva azzal a lehetőséggel, hogy egyes nem szomszédos párok is egységnyi távolságra kerülnek-e. Például a Möbius–Kantor-gráf lerajzolható ily módon.

Az egységtávolsággráf ilyen lazább definíciója alapján minden általánosított Petersen-gráf is egységtávolsággráf (Žitnik, Horvat & Pisanski 2010). A két definíció megkülönböztetése érdekében az olyan gráfok, ahol a síkba rajzoláskor megköveteljük, hogy az anti-élek ne egység hosszúságúak legyenek, nevezhetők szigorú egységtávolsággráfoknak (strict unit distance graphs) (Gervacio, Lim & Maehara 2008).

Például a W₇ kerékgráf egyik küllőjének eltávolításával kapott gráf egységtávolsággráf részgráfja, de nem szigorú egységtávolsággráf; egybevágóságtól eltekintve egyetlen módon lehet a csúcspontokat úgy elhelyezni, hogy a szomszédos csúcsok egységnyi távolságra legyenek, de ez az elhelyezés a két végpontot is egység távolságra helyezi el (Soifer 2008, p. 94).

A matematika megoldatlan problémája: Hány egységtávolság lehet ${\displaystyle n}$ pont között? (A matematika további megoldatlan problémái)

Paul Erdős (1946) tette fel a kérdést, hogy n pont közül hány lehet páronként egységnyi távolságra egymástól. Gráfelméleti fogalmakat használva, mennyire lehet sűrű egy egységtávolsággráf?

A hiperkockagráf ad egy alsó korlátot az egységtávolságokra, ami ${\displaystyle n\log n}$-nel arányos. Egy négyzetrácson megfelelően elhelyezett pontokkal Erdős talált egy javított alsó korlátot:

${\displaystyle n^{1+c/\log \log n},}$

majd 500 dollárt ajánlott annak, aki eldönti, hogy a maximális számú egységtávolságokra található-e ilyen formájú felső korlát (Kuperberg 1992). A legjobb ismert felső korlátot Joel Spencer, Endre Szemerédi, and William Trotter (1984) adta, ami arányos a következőhöz: ${\displaystyle n^{4/3};}$.

Ez a korlát pontok és egységkörök incidenciaszámaként (illeszkedésszámaként) is tekinthető, és közeli kapcsolatban van a pontok és egyenesek illeszkedésével foglalkozó Szemerédi–Trotter-tétellel.

Minden A algebrai számhoz lehetséges találni olyan G egységtávolsággráfot, melyben néhány csúcspont A távolságra található G minden egységtávolsággráf-megfeleltetésében (Maehara 1991, 1992). Ez az eredmény implikálja a Beckman–Quarles-tétel egy véges változatát: bármely egymástól A távolságra lévő p és q pontot tekintve létezik p és q pontokat tartalmazó olyan véges merev egységtávolsággráf, hogy a sík minden olyan transzformációja, ami megtartja az egységtávolságokat a gráfban, egyben megtartja a p és q közötti távolságot is(Tyszka 2000). A teljes Beckman–Quarles-tétel állítása szerint ha egy euklideszi sík (vagy annak magasabb dimenziójú megfelelője) bármilyen transzformációja során az egységtávolságok megmaradnak, akkor az a transzformáció egybevágósági; tehát a végtelen egységtávolsággráf számára, melynek csúcspontjai a sík összes pontjával esnek egybe, bármely gráfautomorfizmus egy izometria (Beckman & Quarles 1953).

Az egységtávolsággráf meghatározása kiterjeszthető magasabb dimenziójú euklideszi terekre. Bármilyen gráf beágyazható egy kellően magas dimenziójú tér pontjaiként; (Maehara & Rödl 1990) megmutatja, hogy az ilyen módon szükséges dimenziószám kétszerese a gráf csúcspontjai maximális fokszámának.

Az egységtávolsággráfhoz és a szigorú egységtávolsággráfhoz szükséges dimenziószám nagyon különböző is lehet. A 2n-csúcsú koronagráf például négy dimenzióba ágyazható oly módon, hogy minden éle egység hosszúságú, de legalább n−2 dimenzió szükséges ahhoz, hogy az élek legyenek az egyetlen egység távolságra lévő csúcstávolságok (Erdős & Simonovits 1980).

NP-nehéz feladat annak eldöntése, hogy adott gráf egységtávolsággráf vagy szigorú egységtávolsággráf-e (Schaefer 2013).

NP-teljes feladat annak eldöntése, hogy egy egységtávolsággráf tartalmaz-e Hamilton-kört, még akkor is, ha a gráf csúcspontjai mind egész koordinátákon helyezkednek el (Itai, Papadimitriou & Szwarcfiter 1982).

• Egységkörlapgráf, olyan síkgráf, ahol két pont között akkor húzódik él, ha távolságuk legfeljebb egy.

• Beckman, F. S. & Quarles, D. A., Jr. (1953), "On isometries of Euclidean spaces", Proceedings of the American Mathematical Society 4: 810–815, DOI 10.2307/2032415.
• Erdős, Paul (1946), "On sets of distances of n points", American Mathematical Monthly 53 (5): 248–250, DOI 10.2307/2305092.
• Erdős, Paul & Simonovits, Miklós (1980), "On the chromatic number of geometric graphs", Ars Combinatoria 9: 229–246. As cited by (Soifer 2008, p. 97).
• Gerbracht, Eberhard H.-A. (2009), Eleven unit distance embeddings of the Heawood graph.
• Gervacio, Severino V.; Lim, Yvette F. & Maehara, Hiroshi (2008), "Planar unit-distance graphs having planar unit-distance complement", Discrete Mathematics 308 (10): 1973–1984, DOI 10.1016/j.disc.2007.04.050.
• Itai, Alon; Papadimitriou, Christos H. & Szwarcfiter, Jayme Luiz (1982), "Hamilton paths in grid graphs", SIAM Journal on Computing 11 (4): 676–686, DOI 10.1137/0211056.
• Kuperberg, Greg (1992), The Erdos kitty: At least $9050 in prizes!, Posting to usenet groups rec.puzzles and sci.math, <http://www.math.niu.edu/~rusin/known-math/93_back/prizes.erd>. Hozzáférés ideje: 2006-09-27 Archiválva 2006. szeptember 29-i dátummal a Wayback Machine-ben.
• Maehara, Hiroshi (1991), "Distances in a rigid unit-distance graph in the plane", Discrete Applied Mathematics 31 (2): 193–200, DOI 10.1016/0166-218X(91)90070-D.
• Maehara, Hiroshi (1992), "Extending a flexible unit-bar framework to a rigid one", Discrete Mathematics 108 (1-3): 167–174, DOI 10.1016/0012-365X(92)90671-2.
• Maehara, Hiroshi & Rödl, Vojtech (1990), "On the dimension to represent a graph by a unit distance graph", Graphs and Combinatorics 6 (4): 365–367, DOI 10.1007/BF01787703.
• Schaefer, Marcus (2013), "Realizability of graphs and linkages", in Pach, János, Thirty Essays on Geometric Graph Theory, Springer, pp. 461–482, DOI 10.1007/978-1-4614-0110-0_24.
• Soifer, Alexander (2008), The Mathematical Coloring Book, Springer-Verlag, ISBN 978-0-387-74640-1.
• Spencer, Joel; Szemerédi, Endre & Trotter, William T. (1984), "Unit distances in the Euclidean plane", in Bollobás, Béla, Graph Theory and Combinatorics, London: Academic Press, pp. 293–308, ISBN 0-12-111760-X.
• Tyszka, Apoloniusz (2000), "Discrete versions of the Beckman-Quarles theorem", Aequationes Mathematicae 59 (1-2): 124–133, DOI 10.1007/PL00000119.
• Žitnik, Arjana; Horvat, Boris & Pisanski, Tomaž (2010), All generalized Petersen graphs are unit-distance graphs, vol. 1109, IMFM preprints, <http://www.imfm.si/preprinti/PDF/01109.pdf>.

• Venkatasubramanian, Suresh, "Problem 39: Distances among Point Sets in R² and R³", The Open Problems Project, <http://maven.smith.edu/~orourke/TOPP/P39.html>. Hozzáférés ideje: 2006-09-26 Archiválva 2006. augusztus 30-i dátummal a Wayback Machine-ben.
• Weisstein, Eric W.: Unit-Distance Graph (angol nyelven). Wolfram MathWorld