Harmônicos esféricos

Em matemática e ciência física, harmónicos esféricos são funções harmónicas que representam a variação espacial de um conjunto ortogonal de soluções da equação de Laplace, quando a solução é expressa em coordenadas esféricas.

Os harmónicos esféricos são importantes em muitas aplicações teóricas e práticas, particularmente em física atómica (uma vez que a função de onda do electrão contém harmónicos esféricos) e na teoria do potencial, tanto no campo gravitacional como na eletrostática.

Introdução

A equação de Laplace em coordenadas esféricas é dada por:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

(Ver também Nabla e laplaciano em coordenadas esféricas). Se nesta expressão considera-se soluções específicas da forma ${\displaystyle f(r,\theta ,\phi )=R(r)Y(\theta ,\varphi )}$, a parte angular Y é chamada harmónico esférico e satisfaz a relação

${\displaystyle {1 \over \sin \theta }{d \over d\theta }\left(\sin \theta {dY(\theta ,\varphi ) \over d\theta }\right)+{1 \over \sin ^{2}\theta }{d^{2}Y(\theta ,\varphi ) \over d\varphi ^{2}}+l(l+1)Y(\theta ,\varphi )=0}$

Se, por sua vez, utiliza-se o método de separação de variáveis para esta equação, pode-se ver que a equação acima admite soluções periódicas nas duas coordenadas angulares (l é um inteiro). Logo, a solução periódica do sistema anterior depende de dois inteiros (l, m) e é dada em termos de funções trigonométricas e dos polinômios associados de Legendre:

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=N\,e^{im\varphi }\,P_{\ell }^{m}(\cos {\theta })}$

Onde: ${\displaystyle Y_{\ell }^{m}}$ é chamada de função harmónica esférica de grau ${\displaystyle \ell }$ e ordem ${\displaystyle m}$; ${\displaystyle P_{\ell }^{m}}$ é o polinómio associado de Legendre; ${\displaystyle N}$ é uma constante de normalização; e ${\displaystyle \theta }$ e ${\displaystyle \varphi }$ representam os parâmetros angulares (respectivamente, o ângulo azimutal ou colatitude e o ângulo polar ou longitude).

As coordenadas esféricas utilizadas neste artigo são consistentes com àquelas usadas pelos físicos, mas diferem das utilizadas pelos matemáticos (ver coordenadas esféricas). Em particular, a colatitude ${\displaystyle \theta }$, ou ângulo polar, assume valores de ${\displaystyle 0\leq \theta \leq \pi }$ e a longitude ${\displaystyle \varphi }$, ou azimute, está na faixa de ${\displaystyle 0\leq \varphi <2\pi }$. Portanto, ${\displaystyle \theta }$ é nulo no Pólo Norte, ${\displaystyle \pi /2}$ no Equador e ${\displaystyle \pi }$ no Pólo Sul.

Quando a equação de Laplace é resolvida em coordenadas esféricas, as condições de periodicidade na fronteira da coordenada ${\displaystyle \varphi }$ e as condições de regularidades nos "Pólos Norte e sul" da esfera condizem com o que foi dito que os números l e m necessários devem ser inteiros que satisfazem ${\displaystyle \ell \geq 0}$ e ${\displaystyle |m|\leq \ell }$.

Normalização

Há várias normalizações utilizadas para as funções harmónicas esféricas. Em física e sismologia essas funções são geralmente definidas como

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )=A_{\ell }^{m}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

onde

${\displaystyle A_{\ell }^{m}={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}}$

Estas funções são ortonormalizadas,

${\displaystyle \int _{\varphi =0}^{2\pi }d\varphi \int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$,

onde δ_aa = 1, δ_ab = 0 se a ≠ b (ver delta de Kronecker). Nas áreas de geodésia e análise espectral utiliza-se

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1)}{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possui um termo linear

${\displaystyle {1 \over 4\pi }\int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,=\delta _{\ell \ell '}\,\delta _{mm'}}$.

No magnetismo, no entanto, usa-se os harmónicos de Schmidt semi-normalizados,

${\displaystyle Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {(\ell -m)! \over (\ell +m)!}}P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }}$

que possuem a seguinte normalização:

${\displaystyle \int _{\varphi =0}^{2\pi }\int _{-1}^{1}d(cos\theta )Y_{\ell }^{m}(\theta ,\varphi ^{*})\,Y_{\ell '}^{m'*}(\theta ,\varphi )\,={4\pi \over (2\ell +1)}\delta _{\ell \ell '}\,\delta _{mm'}}$.

Utilizando a identidade (ver funções associadas de Legendre)

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}}$

pode-se demonstrar que todas as funções harmónicas esféricas normalizadas acima satisfazem

${\displaystyle Y_{\ell }^{m*}(\theta ,\varphi )=(-1)^{m}Y_{\ell }^{-m}(\theta ,\varphi )}$,

onde o símbolo * significa conjugação complexa.

Convenção de fase de Condon-Shortley

Um forte motivo para uma confusão com a definição de harmónicos esféricos é o fator de fase ${\displaystyle (-1)^{m}\,}$, normalmente identificado como a fase de Condon-Shortley na literatura quântica. Na mecânica quântica, é uma prática usual incluir este fator de fase na definição das funções associadas de Legendre, ou anexá-lo à definição de funções harmónicas esféricas. Não há nenhuma exigência da utilização da fase de Condon-Shortley na definição de funções harmónicas esféricas, mas se ela for incluída, então algumas operações no domínio da mecânica quântica serão mais simples. No magnetismo e na geodésia, ao contrário, nunca incluiu-se o fator de fase Condon-Shortley na definição dos harmónicos esféricos.

Expansão em harmónicos esféricos

Os harmónicos esféricos formam um conjunto completo ortonormal de funções e, portanto, formam um espaço vetorial análogo aos vetores unitários da base. Na esfera unitária, todas as funções de quadrado integrável podem, portanto, ser expandidas como uma combinação linear de:

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{\ell }^{m}\,Y_{\ell }^{m}(\theta ,\varphi )}$.

Essa expansão é exata sempre que ${\displaystyle \ell }$ estende-se até o infinito. Haverá um erro de truncamento ao limitar a soma sobre ${\displaystyle \ell }$ numa largura de banda finita ${\displaystyle L}$. Os coeficientes da expansão ${\displaystyle f_{\ell }^{m}}$ podem ser obtidos multiplicando-se a equação pelo conjugado complexo dos harmónicos esféricos, integrando-se sobre um ângulo sólido ${\displaystyle \Omega \!\,}$ e usando-se as relações de ortogonalidade acima. No caso de harmónicos ortonormalizados, obtemos

${\displaystyle f_{\ell }^{m}=\int _{\Omega }f(\theta ,\varphi )\,Y_{\ell }^{m*}(\theta ,\varphi )d\Omega =\int _{0}^{2\pi }d\varphi \int _{0}^{\pi }d\theta \sin \theta f(\theta ,\varphi )Y_{\ell }^{m*}(\theta ,\varphi )}$.

Um conjunto alternativo de harmónicos esféricos para funções reais pode ser obtido a partir do conjunto

${\displaystyle Y_{\ell m}={\begin{cases}Y_{\ell }^{0}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \quad {\mbox{ se }}m=0\\{1 \over {\sqrt {2}}}\left(Y_{\ell }^{m}+(-1)^{m}\,Y_{\ell }^{-m}\right)={\sqrt {2}}NP_{\ell }^{m}(\theta )\cos m\varphi \qquad \quad \quad {\mbox{se }}m>0\\{1 \over i{\sqrt {2}}}\left(Y_{\ell }^{|m|}-(-1)^{|m|}\,Y_{\ell }^{-|m|}\right)={\sqrt {2}}NP_{\ell }^{|m|}(\theta )\sin |m|\varphi \quad {\mbox{ se }}m<0.\end{cases}}}$

Estas funções têm as mesmas propriedades que as funções de normalização complexas dadas anteriormente. Nesta forma, uma função real integrável pode ser expressa como uma soma infinita de harmónicos esféricos

${\displaystyle f(\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }f_{lm}\,Y_{lm}(\theta ,\varphi )}$.

Harmónicos esféricos em física

Seguem-se algumas aplicações dos harmónicos esféricos na física, tanto na eletrostática como na mecânica quântica.

Harmónicos esféricos na eletrostática

O átomo de hidrogênio

O modelo quântico moderno do átomo de hidrogênio assume o elétron em um estado constante de energia tem sua posição distribuída ao redor do núcleo atômico como uma distribuição de probabilidades, cuja variação angular é dada por um harmónico esférico.

Análise espectral

A potência total de uma função ${\displaystyle f}$ é definida na linguagem de processamento de sinais eletrônicos como sendo a integral do quadrado da função dividida pela área varrida por ela. Usando as propriedades de ortonormalização de funções harmónicas esféricas de potência real unitária, é fácil verificar que a potência total de uma função definida na esfera unitária está relacionada aos seus coeficientes espectrais através de uma generalização do teorema de Parseval:

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{l=0}^{\infty }S_{f\!f}(l)}$,

onde

${\displaystyle S_{f\!f}(l)=\sum _{m=-l}^{l}f_{lm}^{2}}$

é definido como o espectro de potência angular. Da mesma forma, pode-se definir a potência cruzada entre duas funções como

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )\,g(\Omega )\,d\Omega =\sum _{l=0}^{\infty }S_{fg}(l)}$,

onde

${\displaystyle S_{fg}(l)=\sum _{m=-l}^{l}f_{lm}g_{lm}}$

é definido como o espectro cruzado neste caso. Se as funções ${\displaystyle f}$ e ${\displaystyle g}$ possuem valor médio igual a zero (ou seja, com coeficientes espectrais ${\displaystyle f_{00}}$ e ${\displaystyle g_{00}}$ nulos), então ${\displaystyle S_{f\!f}(l)}$ e ${\displaystyle S_{fg}(l)}$ representam as contribuições para a variância e covariância da função para ${\displaystyle \ell }$, respectivamente. É comum que o espectro de potência cruzado seja aproximado por uma lei de potências do tipo

${\displaystyle S_{f\!f}(l)=C\,\ell ^{\beta }}$.

Quando ${\displaystyle \beta =0}$, o espectro é "branco", pois cada nível tem potências iguais. Quando ${\displaystyle \beta <0}$, o espectro é chamado de "vermelho", porque não há mais energia nos níveis mais baixos com comprimentos de onda mais longos do que nos níveis mais elevados. Finalmente, quando ${\displaystyle \beta >0}$, o espectro é chamado de "azul".

Teorema da adição

Um resultado matemático de grande interesse e utilidade é chamado teorema da adição para harmónicos esféricos. Se dois vetores r e r' tem coordenadas esféricas ${\displaystyle (r,\theta ,\varphi )}$ e ${\displaystyle (r',\theta ',\varphi ')}$, respectivamente, o ângulo ${\displaystyle \gamma }$ entre eles é dado pela expressão

${\displaystyle \cos \gamma =\cos \theta \cos \theta '+\sin \theta \sin \theta '\cos(\varphi -\varphi ')}$.

O teorema da adição expressa um polinômio de Legendre de ordem ${\displaystyle l}$ no ângulo ${\displaystyle \gamma }$ em termos de produtos de dois harmónicos esféricos com coordenadas angulares ${\displaystyle (\theta ,\varphi )}$ e ${\displaystyle (\theta ',\varphi ')}$:

${\displaystyle P_{l}(\cos \gamma )={\frac {4\pi }{2l+1}}\sum _{m=-l}^{l}Y_{lm}^{*}(\theta ',\phi ')\,Y_{lm}(\theta ,\varphi )}$.

Esta expressão é válida tanto para harmónicos reais como complexos. Entretanto, deve-se ressaltar que a fórmula apresentada anteriormente é válida apenas para harmónicos esféricos ortonormalizados. Harmónicos de potência unitária são necessários para eliminar o fator ${\displaystyle 4\pi }$ da expressão anterior.

Visualizando os harmónicos esféricos

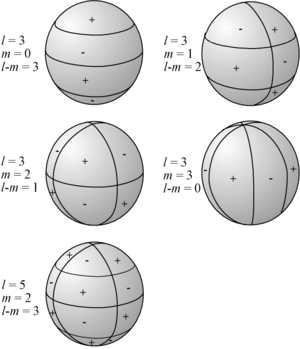
Os harmónicos esféricos são facilmente visualizados através da contagem do número de cruzamentos que ambos estão na direção das coordenadas ${\displaystyle \theta }$ e ${\displaystyle \varphi }$. Para obter a orientação sobre ${\displaystyle \theta }$, as funções associadas de Legendre possuem ${\displaystyle l-|m|}$ zeros, enquanto que na coordenada ${\displaystyle \varphi }$ as funções trigonométricas seno e cosseno possuem ${\displaystyle 2|m|}$ zeros.

Quando o harmónico esférico de ordem ${\displaystyle m}$ é nulo, as funções harmónicas esféricas não dependem de ${\displaystyle \varphi }$, e diz-se que a função é zonal. Quando ${\displaystyle l=|m|}$, não existem zeros na direção ${\displaystyle \theta }$, e diz-se que a função é setorial. Nos outros casos, as funções formam um padrão em xadrez sobre a esfera.

Expressões analíticas para os primeiros harmónicos esféricos

Eis as expressões analíticas dos primeiros harmónicos esféricos ortonormalizados, com a convenção de fase de Condon-Shortley:

${\displaystyle Y_{0}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {1 \over \pi }}}$

${\displaystyle Y_{1}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{-i\varphi }}$

${\displaystyle Y_{1}^{0}(\theta ,\varphi )={1 \over 2}{\sqrt {3 \over \pi }}\,\cos \theta }$

${\displaystyle Y_{1}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {3 \over 2\pi }}\,\sin \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{-2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{-2i\varphi }}$

${\displaystyle Y_{2}^{-1}(\theta ,\varphi )={1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{-i\varphi }}$

${\displaystyle Y_{2}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {5 \over \pi }}\,(3\cos ^{2}\theta -1)}$

${\displaystyle Y_{2}^{1}(\theta ,\varphi )={-1 \over 2}{\sqrt {15 \over 2\pi }}\,\sin \theta \,\cos \theta \,e^{i\varphi }}$

${\displaystyle Y_{2}^{2}(\theta ,\varphi )={1 \over 4}{\sqrt {15 \over 2\pi }}\,\sin ^{2}\theta \,e^{2i\varphi }}$

${\displaystyle Y_{3}^{0}(\theta ,\varphi )={1 \over 4}{\sqrt {7 \over \pi }}\,(5\cos ^{3}\theta -3\cos \theta )}$

Teoria matemática geral

O conjunto dos harmónicos esféricos pode ser visto como uma representação da simetria do grupo das rotações em torno de um ponto SO(3) e das aplicações universais SU(2). Portanto, ele capta a simetria da esfera em duas dimensões. Cada grupo de harmónicos esféricos, com um dado valor do parâmetro l leva a uma representação diferente irredutível do grupo SO(3).

Além disso, a área é equivalente à esfera de Riemann. O conjunto completo das simetrias da esfera de Riemann é descrito pelo grupo das transformações de Möbius PSL(2,C), que é isomorfo ao grupo de Lie real chamado grupo de Lorentz. O análogo dos harmónicos esféricos em relação ao grupo de Lorentz é a série hipergeométrica; na verdade, os harmónicos esféricos podem ser reescritos em termos da série hipergeométrica, já que SO(3) é um subgrupo de PSL(2,C).

Mais especificamente, pode-se generalizar a série hipergeométrica para descrever as simetrias de qualquer espaço de simetria. Em particular, a série hipergeométrica pode ser estendida para todos os grupos de Lie.^[1][2][3][4]

Ver também

• Coeficientes de Clebsch-Gordan
• Função harmónica
• Grupo de rotação
• Teoria de Sturm-Liouville

Referências

• Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em castelhano cujo título é «Armónicos esféricos», especificamente desta versão.

Referencias citadas

Referencias Gerais

• A.R. Edmonds, Angular Momentum in Quantum Mechanics, (1957) Princeton University Press, ISBN 0-691-07912-9.
• E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, (1970) Cambridge at the University Press, ISBN 0-521-09209-4, See chapter 3.
• J.D. Jackson, Classical Electrodynamics, ISBN 0-471-30932-X
• Albert Messiah, Quantum Mechanics, volume II. (2000) Dover. ISBN 0-486-40924-4.
• D. A. Varshalovich, A. N. Moskalev, V. K. Khersonskii Quantum Theory of Angular Momentum,(1988) World Scientific Publishing Co., Singapore, ISBN 9971-5-0107-4

Ligações externas

• Spherical harmonics on Mathworld
• Spherical Harmonic Models of Planetary Topography
• Spherical harmonics generator in OpenGL
• General Solution to LaPlace's Equation in Spherical Harmonics (Spherical Harmonic Analysis). Solid Earth Geophysics.

Software

• SHTOOLS: Fortran 95 software archive
• HEALPIX: Fortran 90 and C++ software archive
• SpherePack: Fortran 77 software archive
• SpharmonicKit