Carnot teoremi (iç yarıçap, dış yarıçap)

Carnot teoremi, bir üçgenin iç teğet çemberi ve çevrel çemberinin yarıçaplarının uzunlukları ile çevrel çemberin merkezinden üçgenin üç kenarına olan mesafelerin toplamı arasındaki ilişkiyi göstermektedir. Fransız matematikçi Lazare Nicolas Marguerite Carnot tarafından bulunmuştur.

Öklid geometrisinde, Carnot teoremi çevrel merkez D'den herhangi bir ABC üçgeninin kenarlarına işaretli mesafelerin toplamının şöyle olduğunu belirtir:

${\displaystyle DF+DG+DH=R+r,\ }$

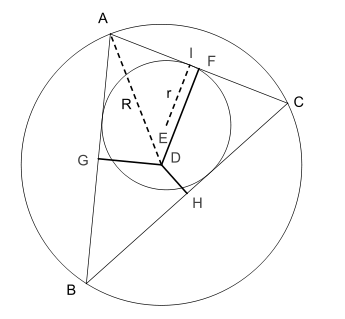
burada r üçgenin iç teğet çemberinin çapı ve R ise çevrel çemberinin çapıdır. Burada mesafelerin işareti, ancak ve ancak açık doğru parçası DX (X = F, G, H) üçgenin tamamen dışında yer alıyorsa, negatif kabul edilir. Şekilde, DF negatiftir ve hem DG hem de DH pozitiftir.

Geniş açılı üçgen	Dar açılı üçgen
${\displaystyle |{\overline {GD}}|+|{\overline {HD}}|-|{\overline {FD}}|=|{\overline {AD}}|+|{\overline {EI}}|=R+r}$	${\displaystyle |{\overline {GD}}|+|{\overline {HD}}|+|{\overline {FD}}|=|{\overline {AD}}|+|{\overline {EI}}|=R+r}$

Teorem, adını Fransız matematikçi Lazare Carnot'dan (1753 – 1823) almıştır. Aynı çember içinde bulunan (concyclic) çokgenler için Japon teoreminin bir kanıtında kullanılır.

Herhangi bir ${\displaystyle \triangle ABC}$'de, çevrel çemberin merkezi ${\displaystyle O}$'dan kenarlara olan (uygun şekilde işaretlenmiş) mesafelerin cebirsel toplamı, çevrel çemberin ve iç teğet çemberin yarıçapların toplamı olan ${\displaystyle R+r}$'ye eşittir.

${\displaystyle OM_{a}+OM_{b}+OM_{c}=R+r}$.

Dar üçgenlerde, çevre merkezi daima üçgenin içinde bulunur. Bu durumda, ${\displaystyle OM_{a}}$, ${\displaystyle OM_{b}}$ ve ${\displaystyle OM_{c}}$'nin üç doğru parçası tamamen üçgenin içinde yer alır. Açılardan biri genişse, çevrel çemberin merkezi üçgenin dışına düşer. Doğru parçalarından biri (geniş açının karşısındaki tarafa karşılık gelen) tamamen dışarıda, diğer iki doğru parçası ise üçgenin yalnızca kısmen dışında uzanır. Yukarıdaki toplamda, üçgenin içini kesen parçalar artı işareti ile, dışta kalan taraf eksi işareti ile alınır. ${\displaystyle OM_{a}}$, ${\displaystyle OM_{b}}$ ve ${\displaystyle OM_{c}}$ doğru parçaları, ${\displaystyle a}$, ${\displaystyle b}$ ve ${\displaystyle c}$ kenarlarındaki tabanlarla ${\displaystyle \triangle OBC}$, ${\displaystyle \triangle OAC}$ ve ${\displaystyle \triangle OAB}$ üçgenlerinin yükseklikleri olarak hizmet eder. İşaret kuralı, bu üçgenlerin alanlarının (uygun işaretlerle birlikte alındığında) her zaman ${\displaystyle \triangle ABC}$ alanını oluşturmasını garanti eder.

Aşağıdaki ispat sadece dar açılı üçgen durumunu ele almış olup, diğer durumlar için de benzer adımlar izlenebilir.

İç teğet çemberin yarıçapı için aşağıdaki ifade her zaman doğrudur:

${\displaystyle r(a+b+c)=2Alan(\triangle ABC)}$.

Yukarıdaki ifadeden,

${\displaystyle Alan(\triangle OAB)+Alan(\triangle OBC)+Alan(\triangle OAC)=Alan(\triangle ABC)}$.

yazılabilir. Bu nedenle,

(*) ${\displaystyle r(a+b+c)=aOM_{a}+bOM_{b}+cOM_{c}}$'dir.

Şimdi sırayla bir açıklama yapalım. ${\displaystyle O}$, ${\displaystyle \triangle ABC}$ üçgeninin çevrel çemberinin merkezi olmak üzere, ${\displaystyle \triangle AOB}$ ikizkenar üçgeninde, ${\displaystyle \angle AOB=2\angle C}$'dir. Ve benzer şekilde, ${\displaystyle \angle BOC=2\angle A}$ ve ${\displaystyle \angle AOC=2\angle B}$'dir. Bu bilgiyle sahip olduğumuzda, benzer (dik açılı) üçgenlerin birkaç üçlüsünü düşünebiliriz:

• ${\displaystyle ABH_{b}}$, ${\displaystyle ACH_{c}}$ ve ${\displaystyle BOM_{a}}$ (veya eşit olan ${\displaystyle COM_{a}}$)
• ${\displaystyle BAH_{a}}$, ${\displaystyle BCH_{c}}$ ve ${\displaystyle COM_{b}}$ (veya eşit olan ${\displaystyle AOM_{b}}$)
• ${\displaystyle CBH_{b}}$, ${\displaystyle CAH_{a}}$ ve ${\displaystyle AOM_{c}}$ (veya eşit olan ${\displaystyle BOM_{c}}$)

İlk üçlüden aşağıdakini türetebiliriz:

${\displaystyle AH_{b}/c=AH_{c}/b=OM_{a}/R}$

bu aşağıdaki sonuca ulaştırır:

${\displaystyle OM_{a}(b+c)=R(AH_{b}+AH_{c})}$

Benzer şekilde, iki ek özdeşlik elde ederiz:

${\displaystyle OM_{b}(a+c)=R(BH_{a}+BH_{c})}$

${\displaystyle OM_{c}(a+b)=R(CH_{a}+CH_{b})}$

Sadeleştirmeden sonra üç eşitlik taraf tarafa toplanırsa:

${\displaystyle OM_{a}(b+c)+OM_{b}(a+c)+OM_{c}(a+b)=R(a+b+c)}$.

elde edilir. Bunu, (*) ifadesi ile toplayıp ${\displaystyle (a+b+c)}$ ifadesine bölersek ispatı tamamlamış oluruz.

Bu ispat için gösterimlerde bir değişiklik gerektiren değiştirilmiş bir şekil üzerinden gidilecektir. Bu kanıt Vaggelis Stamatiadis'e aittir.

${\displaystyle AZOE}$, ${\displaystyle BDOZ}$, ${\displaystyle CEOD}$ dörtgenleri, Batlamyus teoreminin uygulanmasına imkan veren kirişler dörtgenidir:

${\displaystyle OD\cdot BZ+OZ\cdot BD=OB\cdot DZ}$,

${\displaystyle OZ\cdot AE+OE\cdot AZ=OA\cdot EZ}$,

${\displaystyle OE\cdot DC+OD\cdot EC=OC\cdot DE}$

bu aşağıdaki şekilde yazılabilir:

${\displaystyle \displaystyle {\begin{aligned}x{\frac {c}{2}}+z{\frac {a}{2}}&=R{\frac {b}{2}},\\z{\frac {b}{2}}+y{\frac {c}{2}}&=R{\frac {a}{2}},\\y{\frac {a}{2}}+x{\frac {b}{2}}&=R{\frac {c}{2}},\end{aligned}}}$

veya,

${\displaystyle x(b+c)+y(c+a)+z(a+b)=R(a+b+c)\,\iff }$

${\displaystyle x(2s-a)+y(2s-b)+z(2s-c)=2sR\,(2s=a+b+c)\,\iff }$

${\displaystyle 2s(x+y+z)-(ax+by+cz)=2sR\,\iff }$

${\displaystyle 2s(x+y+z)-2[\Delta ABC]=2sR\,\iff }$

${\displaystyle 2s(x+y+z)-2sr=2sR\,\iff }$

${\displaystyle x+y+z=R+r}$.

Diyelim ki, ${\displaystyle A}$ açısı geniş açı ise, uzunluklar arasındaki ilişki ${\displaystyle y+z-x=R+r}$ şeklinde ifade edilir.

• Garreau, G. A. (1946). 1868. Analytical Proof of the Theorems of Carnot and Pascal. The Mathematical Gazette, 30(288), ss. 35-36.
• Ibort, A., de León, M., Lacomba, E. A., Marrero, J. C., de Diego, D. M., & Pitanga, P. (2001). Geometric formulation of Carnot's theorem. Journal of Physics A: Mathematical and General, 34(8), 1691.
• Ðorđe Baralić. (2013), Around the Carnot theorem, Makale 16 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.

• Eric W. Weisstein, Carnot's theorem (MathWorld)
• Carnot's Theorem 10 Eylül 2019 tarihinde Wayback Machine sitesinde arşivlendi. at cut-the-knot
• Carnot's Theorem 17 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. by Chris Boucher. The Wolfram Demonstrations Project.
• Carnot's Theorem 16 Kasım 2020 tarihinde Wayback Machine sitesinde arşivlendi. at artofproblemsolving.com
• Carnot's Theorem 16 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. at gogeometry.com
• Geogebra - Carnot's Theorem
• Carnot's Theorem 19 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. Video (1:49 dk)

• Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009,978-0-88385-342-9, s. 99 25 Aralık 2018 tarihinde Wayback Machine sitesinde arşivlendi.
• Frédéric Perrier: Carnot's Theorem in Trigonometric Disguise.. The Mathematical Gazette, Cilt 91, Sayı 520 (Mart 2007), s. 115–117 (JSTOR 20 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.)
• David Richeson: Konveks Olmayan Çokgenler için Japon Teoremi - Carnot Teoremi 17 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi.. Convergence, Aralık 2013